Function Terminology
Formally, a function from $A$ to $B$ is thought of as a relation $f \subseteq A \times B$.
Definition 58 (Function Terminology).
Let $A$ and $B$ be sets. A relation $f \subseteq A \times B$ is a function from $A$ to $B$ if for each $a \in A$, there is a unique $b \in B$ such that $(a,b) \in f$.
When $f$ is a function from $A$ to $B$, we write $f:A \to B$, and:
- $A$ is the domain of $f$.
- $B$ is the codomain of $f$.
- We write $f(a)=b$ when $(a,b) \in f$.
- The range of $f$ is $$ {b \in B : \exists a \in A \text{ such that } (a,b) \in f} $$ or equivalently $$ {b \in B : \exists a \in A \text{ such that } f(a)=b}. $$
Example functions from ${1,2,3}$ to ${a,b,c}$
${(1,a),(2,b),(3,b)}$ is a function
- domain = ${1,2,3}$
- codomain = ${a,b,c}$
- range = ${a,b}$
${(1,a),(2,b),(2,c)}$ is not a function
- first entry $2$ repeats ⇒ $f(2)$ ambiguous
- no pair with first entry $3$ ⇒ $f(3)$ undefined
${(1,a),(2,a),(3,a)}$ is a constant function
- domain = ${1,2,3}$
- codomain = ${a,b,c}$
- range = ${a}$
Exercise 33
How many functions ${1,2,3} \to {a,b,c}$?
Answer: $3^3 = 27$.
Example functions as pictures
For small sets, we can draw functions:
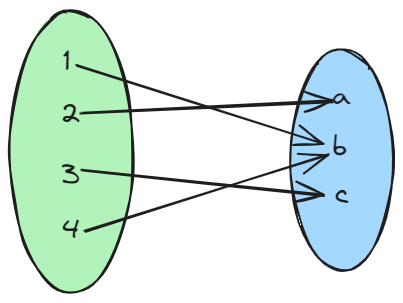
This represents ${(1,b),(2,a),(3,c),(4,b)}$.
For larger sets, functions are usually given by rules.
Example functions with rules
- Example: $f={(x,x^2):x \in \mathbb{R}}$ defines $f:\mathbb{R}\to\mathbb{R}$ by $f(x)=x^2$.
- For any set $A$, the identity function is $I_A={(a,a):a \in A}$.
- Piecewise functions use different rules on subsets of the domain.
Example: define $g:\mathbb{Z}\to\mathbb{Z}$ by $$ g(x) = \begin{cases} \dfrac{x}{2}, & \text{if } x \text{ is even},\[6pt] \dfrac{x-1}{2}, & \text{if } x \text{ is odd}. \end{cases} $$
Checking a function is well-defined
To check $f:A\to B$ is well-defined, verify:
- Each input has exactly one output.
- Each output lies in the codomain.
Pitfalls:
If the domain is $\mathbb{Q}$, we need $f(p/q)=f(2p/2q)$.
Example: $f(p/q)=p$ is not well-defined.If the domain is $\mathbb{Z}/5\mathbb{Z}$, then $[3]=[8]$, so we must have $f([3])=f([8])$.
Exercise 34
Let $g:\mathbb{Z}\to\mathbb{Z}$ be $$ g(x)= \begin{cases} \dfrac{x}{2}, & \text{if } x \text{ is even}, \dfrac{x-1}{2}, & \text{if } x \text{ is odd}. \end{cases} $$
Solution.
- Well-definedness: every integer is even or odd, never both. If $x$ is even, $x/2 \in \mathbb{Z}$. If $x$ is odd, $(x-1)/2 \in \mathbb{Z}$. Exactly one rule applies.
- Range: Claim $\operatorname{ran}(g)=\mathbb{Z}$. For any $n\in\mathbb{Z}$, $g(2n)=n$. So every integer is in the range. Thus the range equals $\mathbb{Z}$.
Composition of Functions
Definition 59 (Composition).
Let $f:A\to B$ and $g:B\to C$. Define
$$
g\circ f = {(a,c)\in A\times C: \exists b\in B,\ (a,b)\in f,\ (b,c)\in g}
= {(a,g(f(a))):a\in A}.
$$
Exercise 35
Write $g\circ f$ as a subset of $A\times C$ and draw the diagram.
Solution.
$$
g\circ f={(1,y),(2,x),(3,x),(4,y)}.
$$
Injective and Surjective Functions
Definition 61 (Injective).
A function $f:A\to B$ is injective if
$$
f(x)=f(y)\ \Rightarrow\ x=y.
$$
Equivalently, if $x\neq y$ then $f(x)\neq f(y)$. Also called one-to-one.
Examples.
- ${(1,a),(2,c),(3,d)}$ is injective ${1,2,3}\to{a,b,c,d}$.
- No injection exists from ${1,2,3}$ to ${a,b}$.
- $f(x)=2x+1$ is injective $\mathbb{Z}\to\mathbb{Z}$:
If $2x+1=2y+1$, then $2(x-y)=0\implies x=y$.
Definition 63 (Surjective).
A function $f:A\to B$ is surjective (onto) if for every $b\in B$, there exists $a\in A$ with $f(a)=b$.